Mathematics (XI): Permutation & Combination

Abdullah Al Mahmud

Permutation

In how many ways can we arrange 3 letters A, B, C?

  • ABC
  • ACB
  • BAC
  • BCA
  • CAB
  • CBA
  • That is, 6 ways. In short \(3!=3 \times 2 \times 1 = 6\)

Arranging Subset

In how many ways can we arrange 2 letters from A, B, C?

  • AB
  • BA
  • AC
  • CA
  • BC
  • CB
  • Again 6 ways, but we get it using \(^3P_2 = \frac{3!}{(3-2)!}=\frac {6}{1!}=6\)

What is 0!

Why is \(3!\ne 3 \times 2 \times 1 \times 0\)?

Rule of Counting

How the counting rule works?

Counting Rule

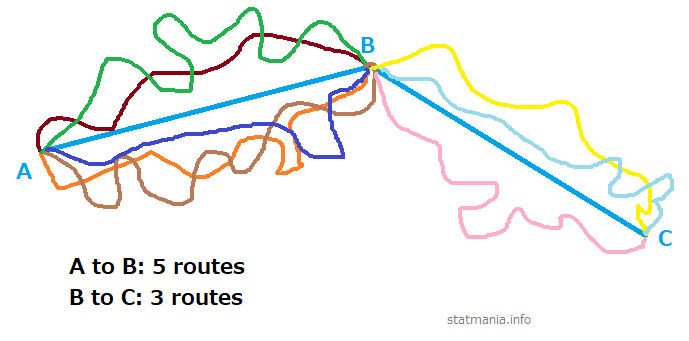
How many possible routes, from A to B, are there?

Example

1.a. In how many ways can you select a team of 15 cricketers from a team of 23 cricketers and then from them a final team of 11 cricketers?

1.b. Afterwards, if you arrange the cricketers in the field, in how many ways can you do the entire process?

Exercises

1(a)

Find the value of n

\(^{n-1}P_3:^{n+1}P_3=5:12\)

1(b)

Find the value of n

\(4 \times ^nP_3 = 5 \times ^{n-1} P_3\)

1(c)

How many different arrangements can you make by using any 3 items from n different items, without using the general formula and without using an item more than once? What if you can use one item multiple times?

2(a)

How many words can be formed using the letters of the word EQUATION?

  • Answer = 8! = 4.03210^{4}

2(c)

Find the n(arrangements) of the words

  1. committee
  2. infinitesimal
  3. proportion

Extra 01

How many arrangements can be made using the letters from the word COURAGE? What if the arrangements must contain a vowel in the beginning?

  • \(4 \times 6!\)

Extra Problem 02

How many arrangements are possible using the words

  • EYE
  • CARAVAN?

3(a)

There are (p+q) items, of which p items are homogeneous and q items are heterogeneous. How many arrangements are possible?

2(j)

There are 10 letters, of which some are homogeneous while others are heterogeneous. The letters can be arranged in 30240 ways. How many homogeneous letters are there?

Let, \(m = \text{number of homogeneous items}\)

  • n(arrangements) = 30240 = \(\frac {10!}{m!}\)
  • \(m! = \frac{10!}{30240}=120\)
  • m = 5

2(k)

A library has 8 copies of one book, 3 copies of another two books each, 5 copies of another two books each and single copy of 10 books. In how many ways can they be arranged?

Total books = \(1 \times 8+3 \times 2+5 \times 2 + 8 \times 1 + 10\) = 42

  • n(arrangements) = \(\frac{42}{8!(3!)^2(5!)^2}\)

2(l)

A man has one white, two red, and three green flags; how many different signals can he produce, each containing five flags and one above another?

Flags: W = 2, R = 2, G = 3, Total = 7

Answer

2 (m)

A man has one white, two red, and three green flags. How many different signals can he make, if he uses five flags, one above another?

3(a)

How many different arragnements can be made using the letters of the word ENGINEERING? In how many of them do the three E’s stand together? In how many do the E’s stand first?

i
ii
iii

3(b)

In how many ways can the letters of the word CHITTAGONG be arranged, so that all vowels are together?

  • Vowels are like one single letter
  • They can switch places between themselves
  • Answer = \(\frac{8!}{2!2!} \times 3!=\) 6.04810^{4}
  • What about TECHNOLOGY, DEPRESSION?

3(e)

In how many ways may 7 green, 4 blue, and 2 red counters be arranged in a row? How many arrangements will have two red counters side by side?

i
ii

3(f)

Five Math books, three Physics books, and two Statistics books are to be arranged in a shelf. In how many ways can they be arranged, if books on same subject are put together?

  • They are like 3 books.
  • Books on individual subjects can still be arranged among themselves.
  • \(3!5!3!2!=\) 8640

4 (a)

Arrange the letters of the word ARRANGE so that two R’s are not together.

  • n(total arrangements) - n(arrangements with T’s together)
  • \(\frac{7!}{2!2!}-\frac{6!}{2!}=\) 900

ENGINEERING (E’s together, first)

In how may are E’s together? In how many are they at the beginning?

Total letters: 11, N=3, G=2, I=2, E=3

Together

Consider 3 E’s one single letter

  • \(\frac{9!}{3!2!2!}\)

Beginning

Placing 3 E’s at the beginning, we have 8 remaining positions.

E E E Other Letters

Balls Apart

There are 7 red and 2 white balls. Arrange by keeping white balls apart.

Without Changing Position

  • Without changing order \(\rightarrow\) Consider them homogeneous
  • Without changing position \(\rightarrow\) Arrange other letters
  1. PERMUTAION, without changing positions of vowels
  2. DIRECTOR, without changing order of vowels
  3. DIRECTOR, without changing positions of vowels
  4. DIRECTOR, without changing relative positions of vowels & consonants

Specific Word at First/Last

  1. MILLENNIUM: M at first & last
  2. IMMEDIATE: T first & A last
  3. DAUGHTER: starts with D
  4. DAUGHTER: starts with D but does not end with R

Even/Odd/middle positions

Questions

  1. POSTAGE: vowels at even positions
  2. ARTICLE: vowels at odd positions
  3. SECOND: Use 1 vowel and 2 consonants & vowel in middle. □ □ □
  4. Make 3-letters words from 7 consonants and 3 vowels so vowels are in middle.
  5. CAMBRIDGE: Use 5 letters including all vowels.
  6. EQUATION: 4-letters words keeping Q excluding N.

Answers

  • 3!4!
  • \(^4P_3 \times 4!=576\)
  • \(^2P_1 \times \space ^4P_2\)
  • \(^3P_1 \times \space ^7P_2=126\)
  • \(^5P_3 \times \space ^6P_2\)
  • \(^4P_1 \times \space ^6P_3\)

Digit Problems

  1. Use \(3,4,5,6,7,8\) to make digits between 5,000 & 6,000.
  2. 2, 3, 4, 5, 6, 7: 6-digit numbers not divisible by 5
  3. 5, 6, 7, 8, 0: Five digit numbers divisible by 4.
  4. Make 7-digit numbers using 3, 4, 5, 5, 3, 4, 5, 6, keeping odd digits at odd positions, without using digits more than its frequency.
  5. Use 1, 2, 3, 4, 5, 6, 7, 8, 9 to make numbers with even digits at beginning and end, using each digit only one.
  6. Form numbers with 0, 3, 5, 6, 8 greater than 4000, without repeating any digit.
  • 4-digits and starts with 5 \(\rightarrow 1 \times \space ^5P_3\)
  • □ □ □ □ □ □ \(\rightarrow 5! \times \space ^5P_1\) or 6!-5!
  • Last two: 56,68, 76 and 60, 08, 80 \(\rightarrow 3! \times ^3P_1 + ^2P_1 \times 2! \times ^3P_1=18+12=30\)
  • Odd positions = 4, even = 3;
    there are repetitions. \(\rightarrow \frac {4!}{2!2!} \times \frac{3!}{2!}=18\)
  • \(^4P_1 \times ^3P_1 \times 7! = 60480\) or \(^4P_2 \times 7!\)
  • □ □ □ □ + □ □ □ □ □ \(\rightarrow ^3P_1 \times ^4P_3 + ^4P_1 \times 4! = 168\)

Digit Problems (Contd.)

  1. Make meaningful odd numbers using the digits 6, 5, 2, 3, 0 once in each number.
  2. Make meaningful even numbers using 5, 3, 2, 6, 0.
  3. Use 1, 2, 3, 4 to make 3 or less-digit numbers by using digits more than once/any no. of times
  • \(^2P_1 \times ^3P_1 \times 3!=36\)
  • 2 at end, 6 at end, 0 at end \(\rightarrow 2 (1 \times 4!-3!)+4!\)
  • 1-digit + 2-digit+3-digit (□ □ □) \(\rightarrow ^4P_1+4 \times 4 + 4^3\)

Summation Basics

\(123 = 3 \times 1 + 2 \times 10 + 1 \times 100\)

  • Value of a number depends on digits it consists of

Arrangements of 1, 2, 3

123

132

231

213

312

321

In all places, each digit is repeated twice (2!)

Sum = 2!(1+2+3)1+2!(1+2+3)10+2!(1+2+3)100 = 2!(1+2+3)(1+10+100)

Sum-Average

  1. Find summation of 3-digits numbers made using 1, 2, & 3 and 4-digits numbers using 1, 2, 3, 4.
  2. Find summation of all possible numbers above 100,00, made using the digits 0, 2, 4, 6, 8.
  3. Sum of all possible numbers using 1, 2, 3, 4, each just once.
  4. Make the general formula to find sum of all possible numbers
  5. Average of 9-digit numbers made using 5 five times and 4 four times.
  6. Find sum of numbers greater than 10,000, using 1, 3, 5, 7, 9
  7. Find sum of all possible numbers, using 1, 3, 5, 7, 9
    1. 2!(1+2+3)(1+10+100) & 3!(1+2+3)1111
    1. 4!(0+2+4+6+8)(1+10+100+1000+10000)-3!(2+4+6+8)(1+10+100+1000)
    1. \(3! (1+2+3+4)(1111)+^3P_2 \times 10 \times 111+ ^3P_1 \times 10 \times 11 + 10\)
    1. \((n-1)! \times D \times \sum_{i=0}^n 10^i\); (D = Sum of digits, n = no. of digits in the numbers made)
    1. \(n=\frac{9!}{5!4!}, \bar X=\frac{}{n}\)
    1. All 5-digit numbers: 4!(1+3+5+7+9)11111=6666600
    1. 1, 2, 3, o4 4 digit numbers: 4!(1+3+5+7+9)11111+…

Specific Items Apart/First/Last

  1. Arrange 5 items out of 10, always keeping 2 specific items.
  2. Make 5-letters words from English alphabet always keeping A & L
  3. Arrange n books keeping two specific books apart.
  4. Arrange n items where two specific items are not at first or last.
  5. Arrange r items from n items so two specific items are neither at first nor at last.

(n-2)
  • \(^5P_2 \times \space ^8P_3\)
  • \(^5P_2 \times \space ^{24}P_3\)
  • n!-2!(n-1)! = (n-1)!(n-2)
  • \(^{n-2}P_2 \times \space (n-2)!\)
  • \(^{n-2}P_2 \times \space ^{n-2}P_{r-2}\)

Arranging in Seats/Positions

  1. Arrange 10 BSC and 14 ISC students so no two BSC students are together.
  2. Arrange p +ve and q \(-ve\) signs (\(p\lt q\)) so \(-ve\) signs are apart.
  3. Arrange a 15-members committee in 15 seats, keeping the chief guest in middle.
  4. Arrange x boys and y girls (x>y), keeping no two girls together.
  5. IDENTITY: I’s and T’s together
  6. Arrange 6 exam scripts so that the best and worst scripts are not together.
  7. Arrange 11 objects (5 black, 6 white) so that a black item is in middle.
    1. \(^{15}P_{10} \times \space 14!\)
    1. \(\frac{^{q+1}P_p}{p!}\)
    1. □ \(\cdot\) □ \(\rightarrow\) (7+7)!
    1. \(^{(x+1)}P_y \cdot x!\)
    1. 6!
    1. 6! - 5!2!
    1. □ □ □ \(^5P_1 \cdot ^{10}P_2\)

Circular Combination

  1. Arrange 8 dancers in circular fashion.
  2. Use 8 pearls in a band to make a necklace.
  3. Arrange 8 science and 7 arts students circularly so no two arts students are together.
  • 7!
  • \(\frac{(8-1)!}{2}\)
  • \(^8P_7 \times \space 7!\)

Combination

Concept

A, B, C

In how many ways can we select 2?

  • AB, AC, BC
  • When making teams \(AB \equiv BA\)

Formulae And Notation

Formulae (Don’t Memorize!)

  • \(^nC_r = {n! \over r!(n-r)!}\)
  • \(^nC_r \times ^rP_r = ^nP_r = ^nP_r \times r!\) (Permutation-combination relationship)
  • \(^{n+1}C_r = ^nC_r + ^nC_{r-1}\)
  • \(^nC_r=?\) (from above, expanding twice up to n-2)
  • \(^nC_r = ^nC_{n-r}\)

Notation

  • \(^nC_r \equiv\) \(n \choose r\)
  • Select 5 people from 6 \(\rightarrow ^6C_5 =\) \(6 \choose 5\)

Expaniosn of \(^nC_r\)

\[\begin{eqnarray} ^{n+1}C_r &=& ^nC_r + ^nC_{r-1} \nonumber \\ \Rightarrow ^nC_r &=& ^{n-1}C_r + ^{n-1}C_{r-1} \nonumber \\ \Rightarrow ^{n+1}C_r &=& ^{n-1}C_r + ^{n-1}C_{r-1} + ^{n-1}C_{r-1} + ^{n-1}C_{r-2} \nonumber \\ \Rightarrow ^{n+1}C_r &=& ^{n-1}C_r + 2^{n-1}C_{r-1} + ^{n-1}C_{r-2} \nonumber \\ \end{eqnarray}\]

  • Similarly, \(^nC_r = ^{n-2}C_r + 2^{n-2}C_{r-1} + ^{n-2}C_{r-2}\)

Theoretical Problems

  1. Prove \(^{n+1}C_r = ^nC_r + ^nC_{r-1}\)
  2. \(^nP_3 + ^nC_3 = 70; n=?\)
  3. Prove \(^nC_r = ^nC_{n-r}\)
  4. Arrange 11 players from 15 players.
    1. n = 5
    1. \(^{15}C{11} \times 11! = ^{15}P_{11}\)

Repeated Items

If out of n items, p items are homogeneous (repeated), then taking r items (\(r \ge p\))

Number of selection options,

\(N=\sum_{i=0}^p\) \(^{n-p}C_{r-i}\)

Example: Combine THESIS taking 4 letters

Method 1

  • n = 6, p = 2, r = 4

Method 2

  • Taking two S’s + All different letters
  • \(^4C_2 + ^5C_4 = 11\)

Repeated Items (Ctd.)

  1. Professor: make words with 4 letters
    1. all different + 2 same, 2 diff + two of 1 kind + another 2 of another kind
  • \(^6C_4 + ^3C_1 \times ^5C_2 + ^3C_2 = 48\)

Conditional Capacity

  1. Form 11-member committe from two groups of 6 & 8 players keeping at least 4 members from 6-members team. How many ways?
  2. Allocate 9 people in 2 cars, whose capacity are 7 & 4.
6-members 8-members Total (11) Combination
4 7 11 \(^6C_4 \times ^*C_7\)
5 6 11
6 5 11

Always In(Ex)cluding

  • Combine r items from n, always including p \(\rightarrow ^{n-p}C_{r-p}\)
  • Combine r items from n, always excluding p \(\rightarrow ^{n-p}C_{r}\)
  • Explain logically

Always In(Ex)cluding Problems

Select 5 books from 12 so 2 books are

  1. always present
  2. never present
    1. \(^{12-2}C_{5-2} = ^{10}C_3 = 120\)
    1. \(^{12-2}C_5 = ^{10}C_5 = 252\)

At least one

Out of n items, take at least one item each time.
  • □ □ □ \(\cdots\) □ Each item can or cannot be taken (having 2 options).
  • \(\rightarrow 2^n - 1\) (1 \(\leftarrow\) no items included)

Alternative

  • \({n \choose 1} + {n \choose 2} + {n \choose 3} + \cdots + {n \choose n}\)
  • \(\{1 + ^nC_1 \cdot 1 + ^nC_2 \} \cdot 1^2+ \cdots 1^n \} -1\)
  • \((1+1)^n-1\)
  • \(2^n - 1\)

At least one (Problems)

  1. Make words with vowels
  2. Invite at least 1 from 6 friends.
    1. \(2^5-1 = 31\)
    1. \(2^6-1\)

Confusion of Order/Together/Position

Arranging the letters of EQUATION by

  1. Maintaining orders or consonants
  • Allowed: EQAUTOIN
  • Not allowed: ETAUQOIN
  1. Keeping consonants together
  • Allowed: EQTNAUOI, QTNAUOIE
  • Not allowed: ETAUQOIN
  1. Without changing positions of consonants
  • Allowed: IQUATEON
  • Not allowed: ENAUQOIQ
  1. Without changing relative positions of consonants and vowels