Measures of Dispersion

Abdullah Al Mahmud

Concept of dispersion

What is Dispersion?

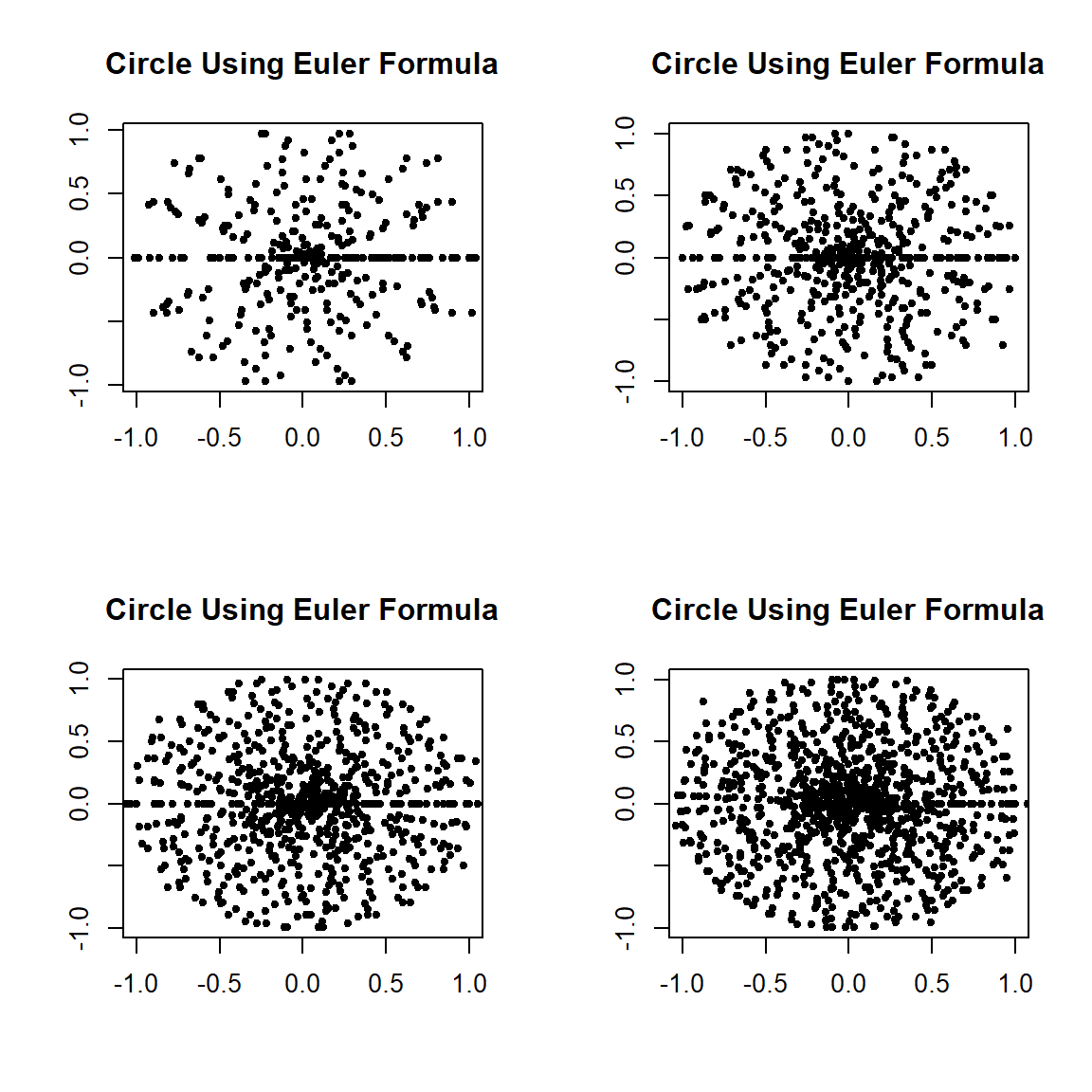
Which plot has the largest dispersion?
Which plot has the smallest dispersion?

Why?

estimate reliability
compare variability of several sets of data
enable further analysis
have a perception of probability

Criteria of A Good Measure

Well-defined
Easy to understand and compute
Based on all observations
Suitable for for further mathematical/statistical analysis
Less affected by sample fluctuation
Unaffected by outliers

Types of Measure

Range

Ungrouped Data Range, \(R = X_H - X_L\)

Grouped Data Range, \(R = R_u - R_l\)

\(L_u\) = Upper boundary of the highest class

\(L_l\) = Lower boundary of the lowest class

\(X=\) 14, 10, 2, 25, 21, 9, 19, 27, 16, 13, 12, 7, 20, 18, 17

Range = 25

Dis(advantages) of Range

Simple & quick
Influenced by outliers
Not suitable for for further mathematical analysis
Cannot be computed for open-ended distribution

Mean Deviation (MD)

Ungrouped Data

\(MD(k)=\frac{\sum_{i=1}^n |x_i-k|} n\), not \(MD(k)=\frac{|\sum_{i=1}^n(x_i-k)|} n\); Beware!

Grouped Data \(MD(k)=\frac{\sum_{i=1}^n f_i|x_i-k|} n\)

k = \[\begin{cases} \bar x, & \text{for MD about mean} \\ \tilde x, & \text{for MD about median} \\ Mo, & \text{for MD about Mode} \end{cases}\]

Compute MD

Compute about mean, median and mode

X = 14, 10, 2, 25, 21, 9, 19, 27, 16, 13, 12, 7, 20, 18, 17

Dis(advantages) of MD

Simple
Unaffected by outliers
Useful for symmetric data only
Not suitable for for further mathematical analysis

Variance and SD

Variance

\[\sigma ^2 = \sum_{i=1}^n \frac{(x_i-\bar x)^2}{n}\]

\(\quad\) = \(\sum \frac{x_i^2}{n}-(\frac{\sum x_i}{n})^2\)

\(\quad\) = Mean of square - square of mean

Standard Deviation (\(\sigma\))

Positive square root of variance

\[\sigma = \sqrt{\sum_{i=1}^n \frac{(x_i-\bar x)^2}{n}}\]
For grouped data?

Variance Estimation

\(x\)	\(x^2\)
12	144
11	121
3	9
\(\sum x = 26\)	\(\sum x^2 = 274\)

\(\sigma^2\)=Mean of square - square of mean

\(\quad\) =\(\bar {x^2}-{\bar x}^2\)

\(\therefore \sigma^2 = \frac{274}{3}-(\frac{26}{3})^2 =\) 24.333
\(\sigma =\) 4.933

Thoughts on Variance?

Think

What is the unit of variance
What is the unit of sd?
Why is variance determined before sd?
What do variance and sd mean?

Dis(advantages) of SD

Variance Example

X = 29, 32, 21, 34, 31, 35, 30, 22

Find variance and stand deviation

Variance, \(\sigma^2=\) 26.786
SD, \(\sigma\) = 5.175

Quartile Deviation(QD)

\(QD=\frac{Q_3-Q_1} 2\)

\(Q_3-Q_1\) is called Interquartile range.

Dis(advantages)

Simple
Unaffected by outliers
Can work with open-ended distribution
Not based on all observations
Not suitable for for further mathematical analysis

Coefficients

- Coefficient of Range,\(CR=\frac{X_H-X_L}{X_H+X_L}\times 100= \frac{\text{Range}}{X_H+X_L}\times 100=\frac{X_u-X_l}{X_u+X_l}\times 100\) (grouped)

Coefficient of Mean Deviation, \(CMD=\frac{MD(\bar x)}{\bar x} \times 100\) (about mean, median and mode similarly)
Coefficient of Variance, \(CV=\frac{\sigma}{\bar x} \times 100\)
Coefficient of Quartile Deviation, \(CQD=\frac{Q_3-Q_1}{Q_3+Q_1} \times 100\)

Compute Coefficients

X = 29, 32, 21, 34, 31, 35, 30, 22

CR = 25
\(CMD(\bar x)\) = 13.462
CV = 17.694
CQD = 8.787

SD vs CV

60 students earned GPA 5 from VNC
45 students earned GPA 5 from Udayan college.

Which college is better?

Average batting score of Soumya = 35
Average batting score of Mushfiq = 34

Who is better?

Use of CV

For estimating skewness, correlation etc.
A measure of consistency/performance

Properties of SD

Depends on scale, but not on origin (prove)
For two unequal observations, \(SD=\frac R 2\); where \(R = Range\)
\(MD \le SD\)
For n positive observations, \(\bar X \sqrt{n-1}\ge \sigma\)
For the first n natural numbers, \(\sigma = \sqrt{\frac{n^2-1}{12}}\)
For two positive observations, \(AM>SD\)
For n number of unequal values, \(\sigma \lt R\)
\(SD \lt \text{Root Mean Square Deviation}\)

Is \(\sigma^2\) alwyas \(\gt \sigma\)

Exceptions

We know, \(\sigma=\sqrt \sigma^2\) (N:B: \(-2=-\sqrt 4; -2\ne \sqrt 4\))

If \(\sigma^2=1, \sigma =1\)
If \(\sigma^2 \lt 1, \sigma ^2 < \sigma\)
Example: \(\sigma^2=0.05, \sigma = \sqrt{0.05} = 0.2236068\)

CV is a Pure Number

No Unit
Absolute number

Minimum Value of \(\sigma\)

\(\sigma \ge 0\)

\(\therefore\) Least value of \(\sigma\) is 0.

\(\Rightarrow \frac{\sum(x_i-\bar x)^2}{n} = 0\)

\(\Rightarrow \sum(x_i-\bar x)^2 = 0\)

\(\Rightarrow (x_1-\bar x)^2 + (x_2-\bar x)^2 + \cdots + (x_n-\bar x)^2= 0\)

\(\therefore (x_1-\bar x)^2 =0, (x_2-\bar x)^2=0, (x_n-\bar x)^2=0\)

\(\Rightarrow x_1=\bar x, x_2=\bar x, x_n=\bar x\)

\(\Rightarrow x_1=x_2= \cdots =x_n\)

\(\therefore\) SD is least (i.e., 0) when all values are equal.

Comparison with Mean

Subject	Bangla	English	Mathematics	Statistics	Average
Student X	70	70	80	72	72.5
Student Y	98	96	48	50	72.5

Who is better?

Theorems

\(\sigma^2\) Origin-Scale

\(\sigma_x^2=\frac{\sum(x_i-\bar x)^2}{n}\)

Let, \(d_i=\frac{x_i-a}{c}\) (a = origin, c = scale)

\[\begin{eqnarray} &\Rightarrow& x_i=a+cd_i \nonumber \\ &\Rightarrow& \bar x = a + c \bar d \nonumber \\ \end{eqnarray}\]

\[\begin{eqnarray} \sigma_x^2&=&\frac{\sum(x_i-\bar x)^2}{n} \nonumber \\ &=& \frac{\sum(a+cd_i-a-c \bar d)^2}{n} \nonumber \\ &=& \frac{\sum(cd_i-c \bar d)^2}{n} \nonumber \\ &=& \frac{c^2\sum(d_i-\bar d)^2}{n} \nonumber \\ &=& c^2 \sigma_d^2 \nonumber \\ \end{eqnarray}\]

\(\therefore \sigma_x^2=c^2 \sigma_d^2\)

Similar procedure and outcome for standard deviation

MD, SD and Range

\(MD=SD=\frac R 2\) for \(x_1\ne x_2\) (two unequal observations)

\(\bar x = \frac {x_1+x_2} 2\) and \(R=|x_1-x_2|\)

Mean Deviation,

\[\begin{eqnarray} MD &=& \frac{\sum_{i=1}^2 |x_i-\bar x|}{2} \nonumber \\ MD &=& \frac{\sum_{i=1}^2 |x_1-\bar x|+|x_2-\bar x|}{2} \nonumber \\ &=& \frac{|x_1-\frac{x_1+x_2} 2|+|x_2-\frac{x_1+x_2} 2|}{2} \nonumber \\ &=& \frac{2|\frac{x_1-x_2}{2}|}{2} \nonumber \\ &=& |x_1-x_2| \nonumber \\ &=& \frac R 2 \nonumber \\ \end{eqnarray}\]

Similar process for SD; Start from SD formula

SD and Range

For two unequal observations, \(SD=\frac R 2\)

\[\begin{eqnarray} SD&=&\sqrt{\frac{\sum_{i=1}^2 (x_i-\bar x)^2}{2}} \nonumber \\ &=& \sqrt{\frac{(x_1-\bar x)^2+(x_2-\bar x)^2}{2}} \nonumber \\ &=&\sqrt{\frac{(x_1-\frac{x_1+x_2} 2)^2+(x_2-\frac{x_1+x_2} 2)^2}{2}} \nonumber \\ &=&\sqrt{\frac{(\frac{x_1-x_2}{2})^2+(\frac{x_2-x_1}{2})^2}{2}}\nonumber \\ &=&\sqrt{\frac{2 (\frac{x_1-x_2}{2})^2}{2}}\nonumber \\ &=&\sqrt{\frac{(x_1-x_2)^2} 2}=\frac{|x_1-x_2|}{2} = \frac R 2 \nonumber \\ \end{eqnarray}\]

Variance of First n Natural Numbers

\[\begin{eqnarray} \sigma^2 &=& \frac{\sum x_i^2}{n} - (\frac{\sum x_i}{n})^2 \nonumber \\ &=& \frac{1^2+2^2+3^2+ \cdots + n^2}{n} - (\frac{1+2+3+ \cdots + n}{n})^2 \nonumber \\ &=& \frac{\frac{n(n+1)(2n+1)}{6}}{n} - (\frac{\frac{n(n+1)}{2}}{n})^2 \nonumber \\ &=& \frac{(n+1)(2n+1)}{6} - (\frac{n+1}{2})^2 \nonumber \\ &=& \frac{n+1}{2} (\frac{2n+1}{3}-\frac {n+1}{2}) \nonumber \\ &=& \frac{n+1}{2} (\frac{4n+2-3n-3}{6}) = \frac{n+1}{2}(\frac{n-1}{6}) = \frac{n^2-1}{12} \nonumber \\ \end{eqnarray}\]

Mean, SD, and CV

\(\bar X \sqrt{n-1}\ge \sigma\) or \(CV \lt 100 \sqrt{n-1}\)

Problem 01

Tow numbers are 10 and 20; Determine Range and CV

Answer

Range, \(R = 20-10=10\)

\(\sigma = \frac R 2 = \frac{10} 2 = 5\)

\(CV = \frac{\sigma}{\bar x} \times 100 = \frac{5}{15} \times 100 = 33.33 \%\)

Find SD & MD (3)

Find SD and MD of three observations: -3, 0, 3

Solution

\[\begin{eqnarray} \sigma&=&\sqrt{\text{Mean of Square - Square of Mean}} \nonumber \\ &=& \sqrt{\frac{9+9}{3}-0}=\sqrt{6}=2.45 \nonumber \\ \end{eqnarray}\]

Missing Numbers for Mean and SD (11)

The mean and SD of 5 observations are 4.4 and \(\sqrt{8.24}\), respectively. If three of the five observations are 1, 2, and 6, find the other two.

Solution

\(\frac{9+x_1+x_2}{5}=4.4\)

\(\therefore x_1+x_2=13\)

Again, \(\frac{1^2+2^2+6^2+x_1^2+2^2}{5}-4.4^2=8.24\)

\(\Rightarrow x_1^2+x_2^2=138-41=97\)

\(\Rightarrow (13-x_2)^2+x_2^2=97\)

\(\Rightarrow 169-26x_2+2x_2^2=97\)

\(\Rightarrow x_2^2-13x_2-36=0\)

\(\therefore x_2=9,4; x_1=4,9\)

Converting Series of Natural Numbers

\(scale, c=\text{Common Difference}\)

\(origin, a = \text{Firts observation - c}\)

Example

\(X = 27, 33, 39, \cdots, 111\)

\(c=33-27 = 6, a = 27-6=21\)

\(Y = \frac{X-21}{6} = \frac{27-21}{6}=1, 2, 3, \cdots, \frac{111-21}{6}=15\)

Thanks

Visit

https://lecture.statmania.info

to see all lecture slides.