8.11 Set Theoretic

8.11.1 Concept

Formulae

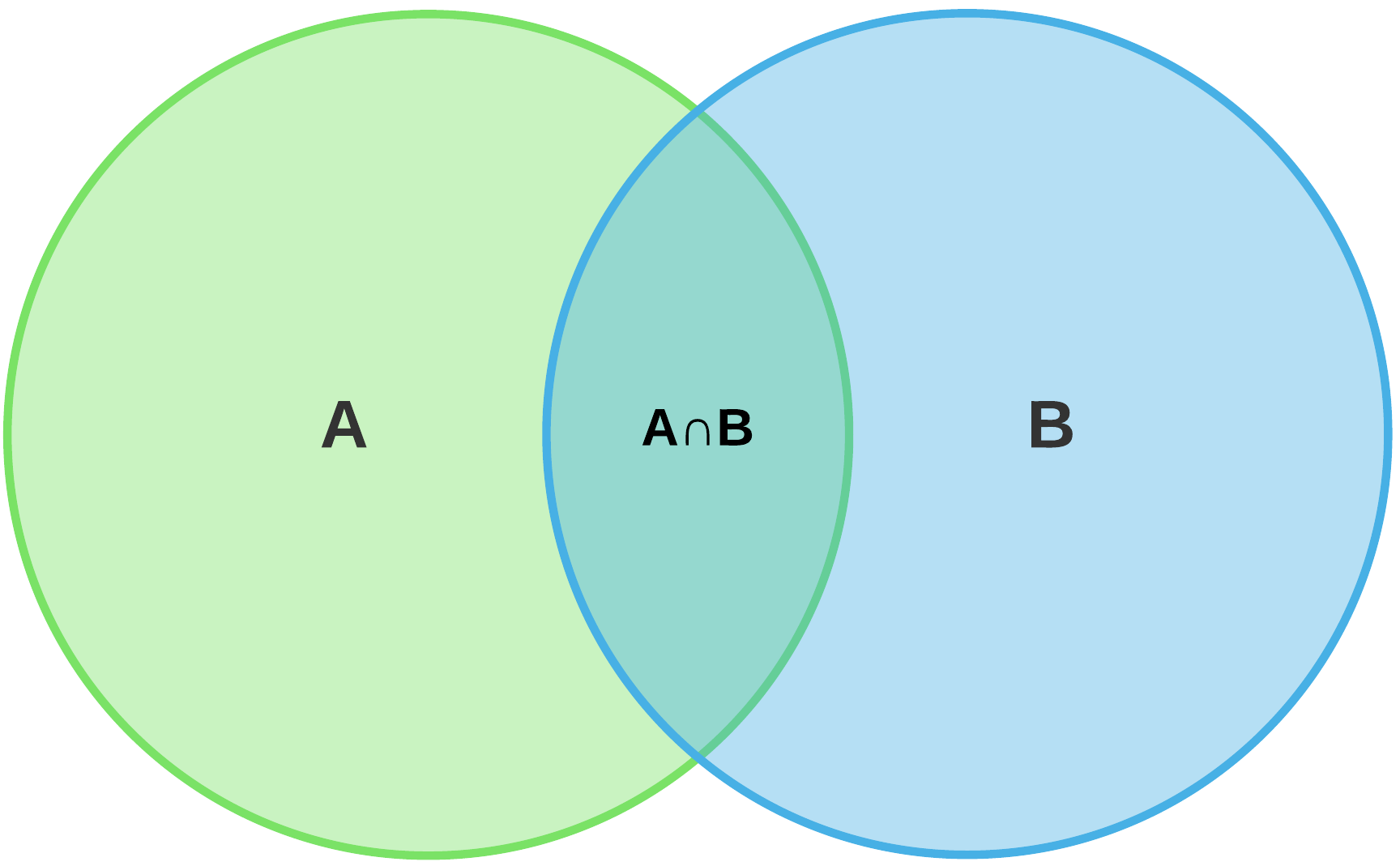
Think Why are they so?

• \(P(A\cap B)=P(A)\times P(B)\), if A & B are independent (prove from Bayes theorem)

• \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)
• \(P(A\cap \bar B)=P(A)-P(A\cap B)\)
• \(P(A|\bar B)=\frac{P(A \cap \bar B)}{P(\bar B)}=?\)
• Also recall De Morgan’s Laws

8.11.2 Set Problem # 01

The probability of Ronaldo scoring a goal is 0.4 and that of Messi 0.38. What is the probability that

1. Both Score
2. Only Ronaldo scores
3. Only Messi scores?
4. At least one of them scores
5. Only one of them scores
6. At most one of them scores

P(R) = 0.4 and P(M) = 0.38

• 1. \(P(R \cap M)=P(R) \times P(M)\) (since independent)
• 2. \(P(R \cap M')=?\)
• 3. \(P(R' \cap M)=?\)
• 4. \(P(R \cup M)\)
• 5. \(P(R \cap M')+P(R' \cap M)\)
• 6. Same to 5

8.11.3 Set Problem # 02

\(S_1\)={1,3,4,7,9,20}

\(S_2\)={12, 13, 14, 15, 16, 17, 18}

If a number is randomly chosen from each set, what is the probability that a prime number comes from \(S_1\) and a multiple of 3 from \(S_2\)?

Solution (click to see)

Say, P = Prime from \(S_1\)

M = Multiple of 3 from \(S_2\).

\(P(P) = \frac 3 7\) and \(P(M)=\frac 3 7\)

What do we need to find out?

• \(P(P \cup M)\)
• \(P(P \cap M)\)

• Answer: \(P(P \cap M) = P(P) \cdot P(M)\)

8.11.4 Set Problem # 03

Cup 01 contains 2 black, 3 red, and 1 pink ball. Cup 2 contains only 1 red ball. A cup is selected randomly. Next, a ball is randomly chosen from that randomly selected cup and placed into the other cup. A ball is then drawn randomly from that second cup. Find the probability that the last ball drawn is a pink one.

• 3 possible cases

1. • 1st cup \(\rightarrow\) pink ball \(\rightarrow\) pink ball from 2nd cup

2. • 1st cup \(\rightarrow\) non-pink ball \(\rightarrow\) pink ball from 2nd cup

3. • 2nd cup \(\rightarrow\) red ball \(\rightarrow\) pink ball from 1st (other) cup

• \((\frac 1 2 \times \frac 1 6 \times \frac 1 2 )+ (\frac 1 2 \times \frac 5 6 \times 0) + (\frac 1 2 \times 1 \times \frac 1 7)\)

8.11.5 Set problem # 04

If a senility researcher discovered that in a population of healthy and diseased elderly people, 14% of the people had senile dementia, 63% had arterioplerotic cerebral degeneration, and 11% had both. What is the probability that a person not having arterioplerotic cerebral degeneration has senile dementia?

8.11.6 Set problem # 05

A candidate applied for three posts in an industry, having 3, 4, and 2 candidates respectively. What is the probability of getting a job by that candidate in at least one post?

Answer

\(P(F)+P(S)+P(T)-P(F\cap S)-P(S\cap T)-P(F\cap T)+P(F\cap S \cap T\)

8.11.7 Set problem # 06

A card is drawn from each of two well-shuffled pack of cards. Find the probability that at least one of them is an ace.

Solution(click to see)

Let,

A = Ace from 1st pack

B = Ace from 2nd pack

\(P(A \cup B)=?\)

\(P(A) = \frac{^4C_1}{^{52}C_1}\)

\(P(B) = P(A)\)

\(P(A\cap B) = P(A) \times P(B)\)

• \(P(A \cup B)=P(A)+P(B) - P(A \cap B)\)

8.11.8 Set problem # 07

\(P(A\cap B)= \frac 1 3, P(A \cup B) = \frac 5 6, and \space P(A) = \frac 1 2\)

Find \(P(B)\) and \(P(B^c)\)

8.11.9 Set problem # 08

\(P(A)= \frac 1 2, P(B) = \frac 1 5, \text{and} \space P(A|B) = \frac 3 8\)

Find \(P(A \cap B), P(B|A)\), and \(P(A \cup B)\)

See a clue

\(P(B|A) = \frac {P(A \cap B)}{P(A)}\)

\(P(A|B) = \frac {P(A \cap B)}{P(B)}\)

\(P(A \cap B) = P(A|B) \times P(B)\)

\(\therefore P(B|A) = \frac{P(A|B) \times P(B)}{P(A)}\)